The budget line and its properties

2024 Author: Howard Calhoun | [email protected]. Last modified: 2024-01-02 13:48

In the title - one of the basic terms of the theory of consumer behavior. What is a budget line? This is a graph that helps to analyze the possibilities, desires of the consumer. Let's talk in more detail about the concept, properties of an object, as well as related terms and phenomena.

Word Definition

The budget line (BL) is a straight line, whose points show sets of goods, for which the allocated budget is spent in full. It crosses the Y and X coordinate axes at points that indicate the largest possible number of products that can be purchased for a particular income at current prices.

Thus, BL demonstrates various combinations of 2 sets of any goods that are bought at a certain profit and a fixed price.

BL Properties

Let's imagine the properties of budget lines.

1. They have only a negative slope. Since the sets of goods located in the BL have the same prices, an increase in the number of purchases of one leads to a reduction in purchases of the other. Recall that a curve showing feedback between two variables always has a negative slope.

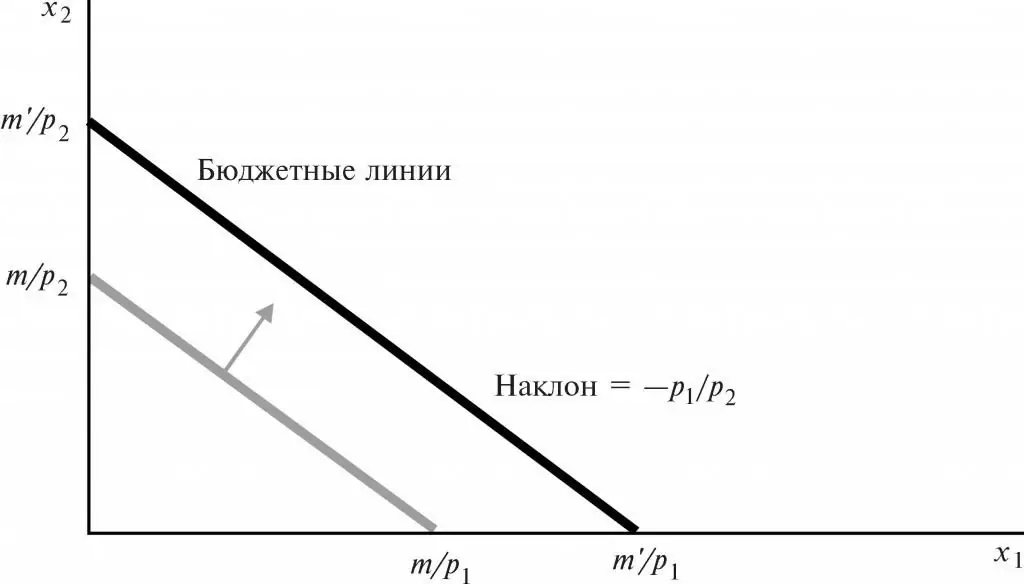
2. The location of the base station depends on the value of the consumer's profit. If his income increases, and prices remain the same, then the budget line will move to the right, parallel to the previous line. If profit decreases at constant prices, then BL goes to the left, but still parallel to the old line.

Thus, a change in the consumer's income will not lead to a change in the angle of inclination of the BL. Only the points of its intersection with the X and Y coordinate axes change.

3. The BL slope coefficient is equal to the ratio of the cost of economic goods with the opposite sign. Let's explain this property. The BL slope coefficient is the ratio of the price of a product, measured horizontally, to the price of a product, measured vertically. Hence the steepness of this slope: P_x /P_{y (price of product X, price of product Y).}

The "minus" sign in this case indicates a negative slope of the BL (after all, the prices for products X and Y will always be only positive values). From here, you need to refrain from buying some item from the X complex in order to purchase something from the Y set.

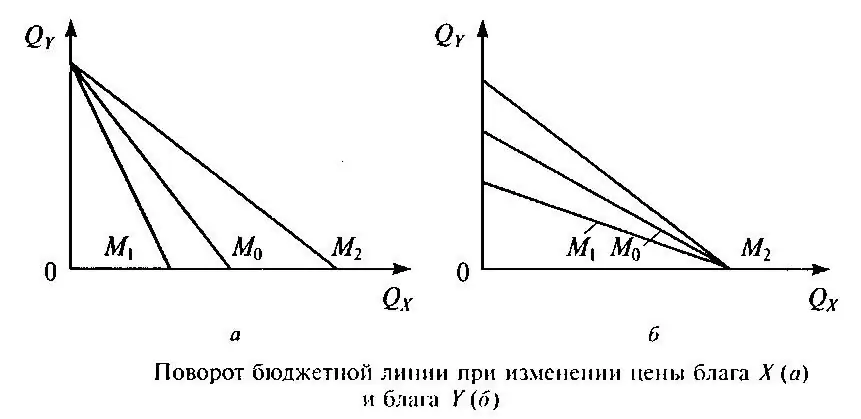
4. A change in the prices of economic goods affects the change in the slope of the BL. Here we see the following. If the cost of one product changes, then the angle of inclination of the budget line and the location of one of the points of intersection of the BL with the coordinate axis change.

But if the prices for both goods become different, then this becomes equivalent to a change in the size of the total profit of the consumer. That is, the BL in this case will move to the right or left.

Budget cap

The budget line is intertwined with broader concepts. The first is the budget constraint. These are all sets of goods that a consumer can buy at a certain budget and current prices. Law of Budget Constraint: Total income equals total expenditure. With any change in the amount of profit, the budget line shifts.

Budget constraint can be described by the equation: P_xQ_x + P_yQ y _{≦ M. Decipher:}

• P_x, P_{y – price of two goods (X and Y).}
• Q_x, Q_{y – some quantity of goods X and Y.}
• M is the budget available to the consumer.
• The sign "less than or equal to" means that the total amount of expenses cannot be more than a person's income. The maximum expenses can be equal to the total profit.

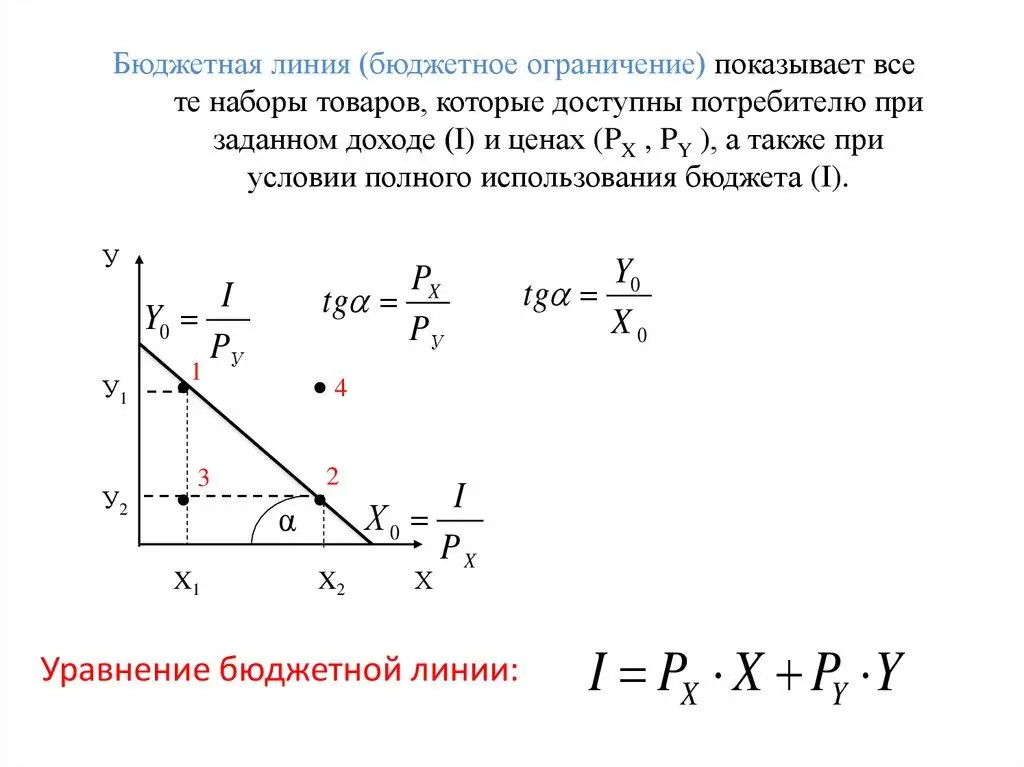
From here it is clear how the BL intersects the X and Y coordinate axes at two points:

• X₁ =M/P_x.
• Y₁ =M/P_y.

These points on the budget line show the maximum amount of products X and Y that can be purchased with the consumer's income at today's prices.

Fiscal space

The next important related concept is budget space. This is the name of the entire selection zone available to the consumer. On the graphs it is represented by a shaded triangle. On the one hand, it is limited by the budget line of the consumer, on the other hand, by the coordinate axes X andW.

To select such a space in the figure, it is enough to construct a straight line of the budget constraint using the formula: P_xQ_x + P _yQ_y=M.

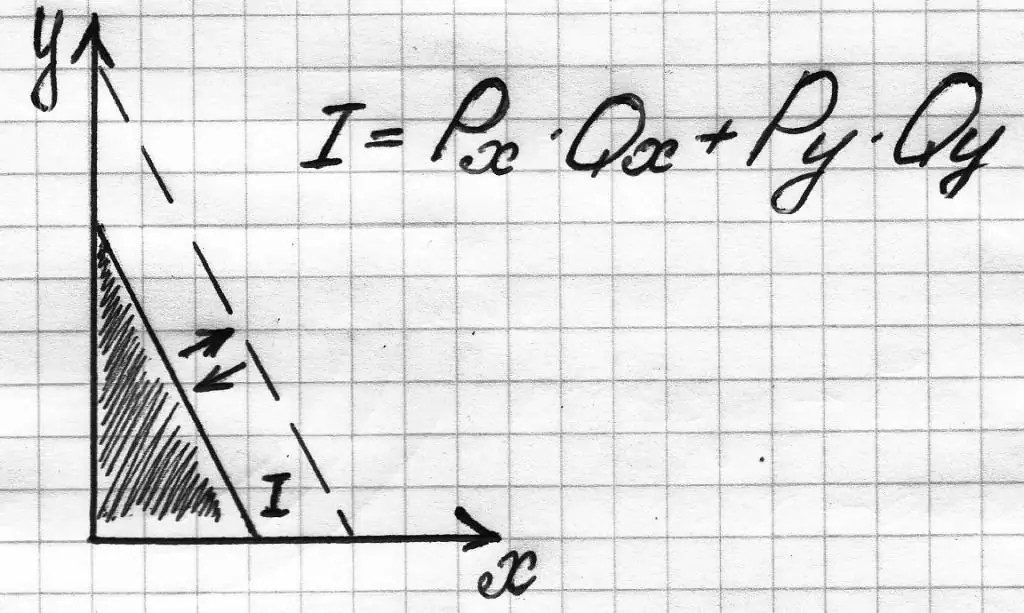
Indifference curve

Indifference curve (indifference curve) - these are different combinations of a pair of economic benefits that are equally necessary for a person. With the help of such graphs, one can show the equilibrium of the consumer - the point of maximizing the total utility, satisfaction from spending one's fixed profit.

Indifference curves are widely used tools of the neoclassical school of economics. In particular, they are applicable in studies of microeconomic situations related to the problem of choice.

The properties of indifference curves (IB) are as follows:

• CB always has a negative slope as rational consumers prefer more to less.
• CB above and to the right of the other curve is preferred by the consumer.
• CB have a concave shape - it is determined by marginal declining rates of substitution.
• Complexes of goods on curves that are more distant from the origin of coordinates are preferable to sets on curves X and Y axes closer to zero.
• CBs cannot overlap. They demonstrate marginal declining rates of substitution of one product for another.

The CB complex forms a map of the set of indifference curves. It is used to describe consumer preferences for all types of economic goods.

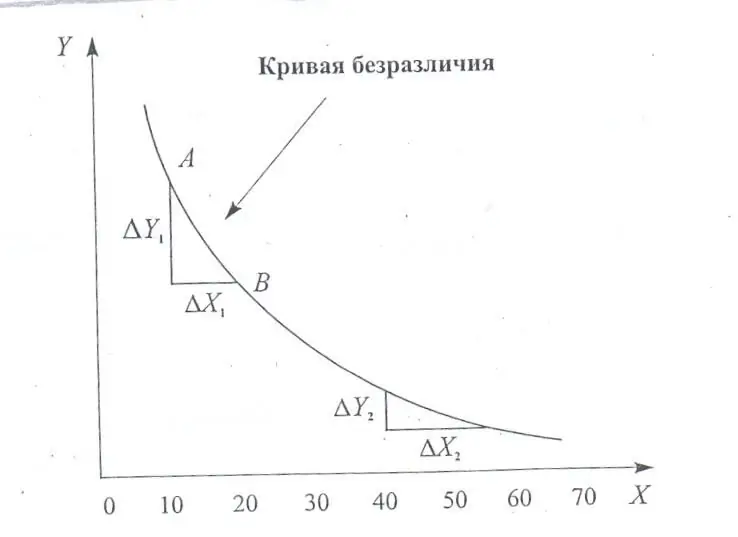
Indifference curves and budget line

How do these concepts relate to each other? An indifference curve shows what a person would like to buy. And BL - what he can get. Together they answer the question: "How can you get the most satisfaction from a purchase with limited profit?"

Thus, CB and BL are used to graphically represent a situation where a person maximizes the utility he acquires when buying two goods with a limited budget. From here it is possible to isolate the requirements of the optimal set of consumer goods. There are only two of them:

• Finding a set of goods on the curve of the budget line.
• Providing the consumer with the most preferred combination.

Thus, the budget line helps to imagine the ratios in which two different sets of economic goods can be purchased for a fixed budget. This graph is often analyzed along with the indifference curve and other related phenomena.